Adding Models to OpenCMP

The OpenCMP code base is designed such that new models can be added without significantly modifying the main code base. All models are kept in the “models” directory and are subclasses of Model. In general, flow models are also further subclassed from INS.

To add a new model construct an appropriate subclass with the following methods. Then modify “models/misc.py” to include the new model. Methods not discussed in the following sections are defined by Model and should not in general be overwritten.

Initialization

_define_model_components

This method returns a a dictionary containing the names of the model variables and their ordering in the finite element space. Convention for flow models is for velocity to be first followed by pressure and any extra components.

_define_time_derivative_components

This method returns a list of dictionaries, keys are variable names and values are bool, indicating which varibles have a time derivative in each

_define_model_local_error_components

This method returns a dictionary noting which model variables are included in local error calculations for adaptive time-stepping. Generally all model variables should be included.

_define_num_weak_forms

This function returns an integer indicating how many different weak forms are used when solving the model. This will only be greater than one for highly nonlinear models that require iterating solves between different model variables (ex: solve velocity holding phase fraction constant then solve phase fraction holding velocity constant all during one single time step).

_pre_init

This function is called AFTER _define_num_weak_forms, _define_model_components, _define_model_local_error_components, and _define_time_derivative_components but BEFORE the rest of __init__(). This is used for setting up model-specific things, such as loading the extra components in mcins.

_post_init

This function is for doing any final model-specific setup after the entire __init__() function has run. For a non-linear model this may include loading self.linearize and various other linearization parameters from the main configuration file (see for example “models/ins”).

_add_multiple_components

This method loads model variable names from the main configuration file. It is only needed if the total set of model variables is not known a prior (ex: a multi-component model that may have any number of different components).

_construct_fes

This method constructs the finite element space for the model. Note that the ordering of the finite element spaces for the different model variables must follow the order stated in self.model_components. Certain finite element spaces are best used with the discontinuous Galerkin method (HDiv) and current practice is to warn users if they choose to use these finite element spaces without the standard continuous finite element method.

_construct_linearization_terms

Any nonlinear models must be linearized in order to be solved by the linear solvers available in OpenCMP. Currently Oseen-style linearization and IMEX-style linearization are used (see for example “models/ins.py”). This method defines the known fields used by Oseen-style linearization.

_define_bc_types

This method returns a list containing the names of all allowable BC types for this model.

_set_model_parameters

This method loads the model parameters and model functions from the “model_config” configuration file. In general, consistent naming should be used across models (ex: all flow models should use “kinematic_viscosity” as the configuration file parameter name). Configuration file parameter names should also be long and descriptive to prevent user confusion (ex: “kv” would be a very unclear configuration file parameter name but is fine as a variable name within the model code).

allows_explicit_schemes

Certain models are unsuited to fully explicit schemes. This method dictates whether or not OpenCMP will allow the use of a fully explicit scheme for the model.

update_linearization_terms

This is a helper method to ensure the linearization terms can be updated correctly at each time step by some of the more complex time-stepping schemes. This method is only needed for nonlinear models and in general should just be copied from the implementation in “models/ins.py” (if the model does not already inherit from INS).

Bilinear Form(s)

As discussed in Time Discretization Schemes, if the model only includes time derivatives for some model variables only weak form terms involving solely those model variables should be discretized by high-order time discretization schemes. All model variables without time derivatives should be discretized following the implicit Euler scheme regardless of the overall time discretization scheme chosen. In OpenCMP, these different weak form terms are constructed by separate model methods.

Consider for example the incompressible Navier-Stokes equations - with Oseen-style linearization - discretized by the second-order Crank-Nicolson scheme:

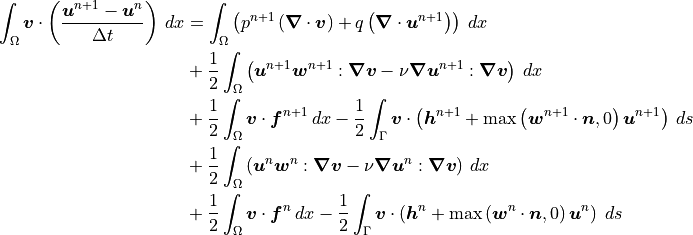
\int_{\Omega} \bm{v} \cdot \left( \frac{\bm{u}^{n+1} - \bm{u}^n}{\Delta t} \right) \: dx &= \int_{\Omega} \left( p^{n+1} \left( \bm{\nabla} \cdot \bm{v} \right) + q \left( \bm{\nabla} \cdot \bm{u}^{n+1} \right) \right) \: dx \\ &+ \frac{1}{2} \int_{\Omega} \left( \bm{u}^{n+1} \bm{w}^{n+1} : \bm{\nabla} \bm{v} - \nu \bm{\nabla} \bm{u}^{n+1} : \bm{\nabla} \bm{v} \right) \: dx \\ &+ \frac{1}{2} \int_{\Omega} \bm{v} \cdot \bm{f}^{n+1} \: dx - \frac{1}{2} \int_{\Gamma} \bm{v} \cdot \left( \bm{h}^{n+1} + \max \left( \bm{w}^{n+1} \cdot \bm{n}, 0 \right) \bm{u}^{n+1} \right) \: ds \\ &+ \frac{1}{2} \int_{\Omega} \left( \bm{u}^{n} \bm{w}^{n} : \bm{\nabla} \bm{v} - \nu \bm{\nabla} \bm{u}^{n} : \bm{\nabla} \bm{v} \right) \: dx \\ &+ \frac{1}{2} \int_{\Omega} \bm{v} \cdot \bm{f}^{n} \: dx - \frac{1}{2} \int_{\Gamma} \bm{v} \cdot \left( \bm{h}^{n} + \max \left( \bm{w}^{n} \cdot \bm{n}, 0 \right) \bm{u}^{n} \right) \: ds

Pressure does not have a time derivative, so all terms containing pressure are discretized with the implicit Euler scheme (right side of line 1). Velocity does have a time derivative, so the terms involving only velocity or boundary conditions are discretized by the Crank-Nicolson scheme (left side of line 1 and lines 2-5).

All models should have a standard Galerkin finite element formulation and a discontinuous Galerkin formulation, as well as diffuse interface formulations for both. Current practice, to avoid long convoluted methods, is to provide each of these formulations as separate functions and then call the desired ones (as specified in the main configuration file) within construct_bilinear_time_ode and construct_bilinear_time_coefficient.

Furthermore, some models will have multiple weak forms that they cycle through during each solve. For example, a multi-phase model may iterate between solving for velocity and pressure holding the phase fraction constant then solving for the phase fraction holding velocity and pressure constant over the course of a single time step. In these cases, multiple weak forms must be defined to account for the changing unknowns and returned by construct_bilinear_time_ode and construct_bilinear_time_coefficient in the order in which they should be solved.

construct_bilinear_time_ode

This method constructs the portion of the bilinear form that will be discretized with the overall time discretization scheme. In the example above that would be lines 2 and 4. Note that the time derivative term is handled by a separate method.

construct_bilinear_time_coefficient

This method constructs the portion of the bilinear form containing model variables without time derivatives. In the example above that would be the right side of line 1.

construct_linear

This method constructs the linear form excluding any terms from IMEX-style linearization.

All models should have a standard Galerkin finite element formulation and a discontinuous Galerkin formulation, as well as diffuse interface formulations for both. Current practice, to avoid long convoluted methods, is to provide each of these formulations as separate functions and then call the desired ones (as specified in the main configuration file) within construct_linear.

Furthermore, some models will have multiple weak forms that they cycle through during each solve. For example, a multi-phase model may iterate between solving for velocity and pressure holding the phase fraction constant then solving for the phase fraction holding velocity and pressure constant over the course of a single time step. In these cases, multiple weak forms must be defined to account for the changing unknowns and returned by construct_linear in the order in which they should be solved.

construct_imex_explicit

This method constructs the portion of the linear form added due to IMEX-style linearization. It is only used by nonlinear models. Like the methods for constructing the bilinear form and linear form this method must account for standard Galerkin finite element, discontinuous Galerkin, and diffuse interface model formulations as well as potentially multiple model weak forms.

solve_single_step

This method runs one single time step of the model possibly including iterations for Oseen-style linearization or iterations between different model weak forms. In the case of a stationary solve, this method solves for the steady state solution.