Time Discretization Schemes

The time-stepping schemes used in OpenCMP can be split between those used with fixed time steps and those used for adaptive time-stepping. Each category can be further split into single-step, multi-step and Runge-Kutta schemes. Finally, these further categories can be split by the type of linearization done. At present, the only nonlinear model is incompressible Navier-Stokes, which can be linearized either as the Oseen equation or by using an IMEX time-stepping scheme.

Definitions

Single-Step Schemes: Use only the values at the previous time step.

Multi-Step Schemes: Use the values from several previous time steps (require storing information from several previous time steps).

Runge-Kutta Schemes: Use only the values at the previous time step, but take one or more intermediate steps within a time step.

IMEX Schemes: Split a nonlinear equation into the nonlinear terms 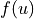$f(u)$ and the linear terms 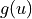$g(u)$ . The nonlinear terms are solved explicitly to avoid the need for a nonlinear solver while the linear terms are still solved implicitly. Typically the linear terms are very stiff and would severely limit the time step if solved explicitly.

Notation

For the remainder of this document the governing equation to be solved will be taken as

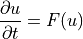
$\frac{\partial u}{\partial t} = F(u)$

When discussing IMEX schemes 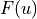$F(u)$ can be split as

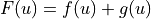
$F(u) = f(u) + g(u)$

where, as above, 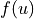$f(u)$ represents the nonlinear terms and 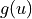$g(u)$ represents the linear terms.

The variable values at each time step will be denoted by a superscript. For example, 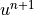$u^{n+1}$ is the value of 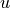$u$ to be solved for at the next time step, while 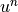$u^n$ is the known value of 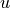$u$ from the previous time step.

The time step will be denoted as 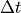$\Delta t$ , again with a superscript if it changes at each time step as with an adaptive time-stepping scheme.

Fixed Time Step Schemes

The following time-stepping schemes have been implemented for use with a fixed time step.

Implicit Euler

Implicit Euler is a first-order accurate single-step scheme.

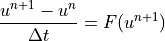
$\frac{u^{n+1} - u^n}{\Delta t} = F(u^{n+1})$

Explicit Euler

Explicit Euler is a first-order accurate single-step scheme.

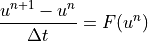
$\frac{u^{n+1} - u^n}{\Delta t} = F(u^n)$

Crank-Nicolson (Trapezoidal Rule)

Crank-Nicolson is a second-order accurate single-step scheme.

$\frac{u^{n+1} - u^n}{\Delta t} = \frac{1}{2} \left[ F(u^{n+1}) + F(u^n) \right]$

First-Order IMEX (Euler IMEX)

Euler IMEX is a first-order accurate single-step IMEX scheme. This could also be considered a first-order SBDF scheme.

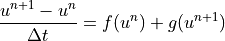
$\frac{u^{n+1} - u^n}{\Delta t} = f(u^n) + g(u^{n+1})$

CNLF (Crank-Nicolson Leap-Frog)

CNLF is a second-order accurate multi-step IMEX scheme.

$\frac{u^{n+1} - u^{n-1}}{2\Delta t} = f(u^n) + \frac{1}{2} \left[ g(u^{n+1}) + g(u^{n-1}) \right]$

SBDF (Semi-Implicit Backwards Difference)

SBDF is a third-order accurate multi-step IMEX scheme. SBDF can also refer to a family of IMEX schemes of various orders, but only the third-order scheme has been implemented in OpenCMP.

$\frac{1}{\Delta t} \left[ \frac{11}{6} u^{n+1} - 3 u^n + \frac{3}{2} u^{n-1} - \frac{1}{3} u^{n-2} \right] = 3f(u^n) - 3f(u^{n-1}) + f(u^{n-2}) + g(u^{n+1})$

(2,3,2)

(2,3,2) is a second-order accurate Runge-Kutta IMEX scheme.

First Intermediate Step: 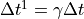$\Delta t^1 = \gamma \Delta t$

$\frac{u^1 - u^n}{\Delta t} = \gamma \left[ f(u^n) + g(u^1) \right]$

Second Intermediate Step: 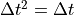$\Delta t^2 = \Delta t$

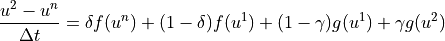
$\frac{u^2 - u^n}{\Delta t} = \delta f(u^n) + (1-\delta) f(u^1) + (1-\gamma) g(u^1) + \gamma g(u^2)$

Final Solve for $u^{n+1}$ :

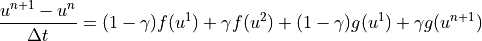
$\frac{u^{n+1} - u^n}{\Delta t} = (1-\gamma) f(u^1) + \gamma f(u^2) + (1-\gamma) g(u^1) + \gamma g(u^{n+1})$

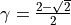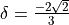The implemented scheme uses $\gamma = \frac{2 - \sqrt{2}}{2}$ and $\delta = \frac{-2\sqrt{2}}{3}$ .

(2,2,2)

(2,2,2) is a second-order accurate Runge-Kutta IMEX scheme.

Intermediate Step: 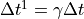$\Delta t^1 = \gamma \Delta t$

$\frac{u^1 - u^n}{\Delta t} = \gamma \left[ f(u^n) + g(u^1) \right]$

Final Solve for 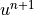$u^{n+1}$ :

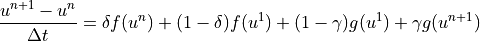
$\frac{u^{n+1} - u^n}{\Delta t} = \delta f(u^n) + (1-\delta) f(u^1) + (1-\gamma) g(u^1) + \gamma g(u^{n+1})$

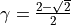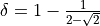The implemented scheme uses $\gamma = \frac{2-\sqrt{2}}{2}$ and $\delta = 1-\frac{1}{2 - \sqrt{2}}$ .

Adaptive Time-Stepping Schemes

The following adaptive time-stepping schemes have been implemented.

Adaptive Two Step

This scheme compares a Crank-Nicolson solve to an implicit Euler solve in order to constrain local error. If the time step is accepted the implicit Euler solution is taken as the time step’s solution in order to preserve stability.

Adaptive Three Step

This scheme compares one solve of implicit Euler with two solves of implicit Euler each using 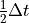$\frac{1}{2} \Delta t$ in order to constrain local error. If the time step is accepted the second implicit Euler solve using 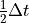$\frac{1}{2}\Delta t$ is taken as the time step’s solution for highest accuracy.

Adaptive IMEX

This scheme defines several new operators.

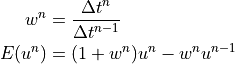
$w^n &= \frac{\Delta t^n}{\Delta t^{n-1}} \\ E(u^n) &= (1 + w^n) u^n - w^n u^{n-1}$

It also uses the explicitly skew-symmetric form of the convection term in incompressible Navier-Stokes

$\frac{1}{2} \left[ \underline{u} \cdot \underline{\nabla} \underline{u} + \underline{\nabla} \cdot \left( \underline{u} \underline{u} \right) \right]$

This is not used in the OpenCMP implementation because it was introducing large errors when 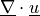$\underline{\nabla} \cdot \underline{u}$ was not exactly zero.

Predictor:

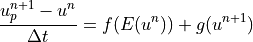
$\frac{u^{n+1}_p - u^n}{\Delta t} = f(E(u^n)) + g(u^{n+1})$

Corrector:

$u^{n+1}_c = u^{n+1}_p - \frac{w^n}{2w^n + 1} \left[ u^{n+1}_p - E(u^n) \right]$

There are also two local error estimators.

$e_1 &= \lvert \lvert u_c^{n+1} - u_p^{n+1} \rvert \rvert \\ e_2 &= \lvert \lvert \frac{w^{n-1} w^n (1 + w^n)}{1 + 2w^n + w^{n-1} (1 + 4w^n + 3(w^n)^2)} \\ &\left[ u^{n+1}_c - \frac{(1+w^n)(1+w^{n-1}(1+w^n))}{1+w^{n-1}} u^n + w^n(1+w^{n-1}(1+w^n)) u^{n-1} - \frac{(w^{n-1})^2 w^n(1+w^n)}{1+w^{n-1}} u^{n-2} \right] \rvert \rvert$

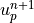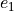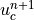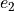A time step’s solution is accepted if either local error estimate is below the user-specified tolerance. The next time step is chosen using the highest local error estimate that satisfies the tolerance. The time step’s solution is taken as $u_p^{n+1}$ if $e_1$ is the highest still-acceptable local error estimate or $u_c^{n+1}$ if $e_2$ is the highest still-acceptable local error estimate.

Models with Multiple Variables

Many models implemented in OpenCMP include dependent variables some of which may not have time derivatives. For example, the incompressible Navier-Stokes equations have a time derivative for velocity but not for pressure:

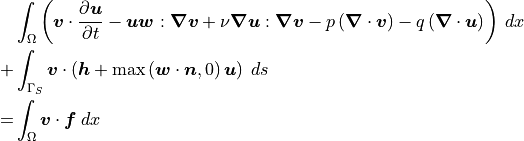
$&\int_{\Omega} \left( \bm{v} \cdot \frac{\partial \bm{u}}{\partial t} - \bm{u} \bm{w} : \bm{\nabla} \bm{v} + \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \: dx \\ + &\int_{\Gamma_S} \bm{v} \cdot \left( \bm{h} + \max \left( \bm{w} \cdot \bm{n}, 0 \right) \bm{u} \right) \: ds \\ = &\int_{\Omega} \bm{v} \cdot \bm{f} \: dx$

where the above formulation uses Oseen-style linearization.

Since pressure has no time derivative it should not be included in the main time discretization scheme. This is apparent with the use of second-order or higher time discretization schemes. Consider, for example, the Crank-Nicolson scheme:

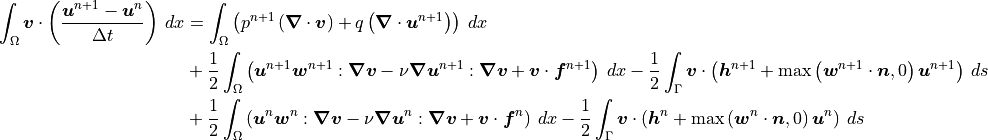
$\int_{\Omega} \bm{v} \cdot \left( \frac{\bm{u}^{n+1} - \bm{u}^n}{\Delta t} \right) \: dx &= \int_{\Omega} \left( p^{n+1} \left( \bm{\nabla} \cdot \bm{v} \right) + q \left( \bm{\nabla} \cdot \bm{u}^{n+1} \right) \right) \: dx \\ &+ \frac{1}{2} \int_{\Omega} \left( \bm{u}^{n+1} \bm{w}^{n+1} : \bm{\nabla} \bm{v} - \nu \bm{\nabla} \bm{u}^{n+1} : \bm{\nabla} \bm{v} + \bm{v} \cdot \bm{f}^{n+1} \right) \: dx - \frac{1}{2} \int_{\Gamma} \bm{v} \cdot \left( \bm{h}^{n+1} + \max \left( \bm{w}^{n+1} \cdot \bm{n}, 0 \right) \bm{u}^{n+1} \right) \: ds \\ &+ \frac{1}{2} \int_{\Omega} \left( \bm{u}^{n} \bm{w}^{n} : \bm{\nabla} \bm{v} - \nu \bm{\nabla} \bm{u}^{n} : \bm{\nabla} \bm{v} + \bm{v} \cdot \bm{f}^{n} \right) \: dx - \frac{1}{2} \int_{\Gamma} \bm{v} \cdot \left( \bm{h}^{n} + \max \left( \bm{w}^{n} \cdot \bm{n}, 0 \right) \bm{u}^{n} \right) \: ds$

Terms involving solely velocity or boundary conditions are discretized following the standard Crank-Nicolson scheme, but terms involving pressure are treated fully implicitly and effectively discretized with the implicit Euler scheme.

There is no clear justification for this treatment of terms without time derivatives in the literature, though it is mentioned in some papers (ex: John2006 A Comparison of Time-Discretization/Linearization Approaches for the Incompressible Navier-Stokes Equations). Current understanding is that since pressure has no time derivative it acts as a constraint on the change in velocity over time but is itself unaffected by the pressure profile at previous time steps. Furthermore, from testing, this treatment of pressure is needed to obtain the expected time step convergence rates from high-order time discretization schemes.

References

First-order IMEX, CNLF, and SBDF are taken from Ascher1995 Implicit-Explicit Methods for Time-Dependent PDEs

(2,3,2) and (2,2,2) are taken from Ascher1997 Implicit-Explicit Runge-Kutta Methods for Time-Dependent Partial Differential Equations

Adaptive IMEX is taken from DeCaria2021 An Embedded Variable Step IMEX Scheme for the Incompressible Navier-Stokes Equations