Models
The following models are currently implemented in OpenCMP. In general, all models are expected to include a standard Galerkin finite element method formulation, a discontinuous Galerkin formulation, and a diffuse interface formulation. Nonlinear models are further expected to include formulations for Oseen-style linearization and IMEX linearization. The following sections provide the weak forms for all implemented formulations of the available models.
Poisson Equation
The Poisson equation takes the following form on a simulation domain 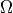 . There are three possible types of boundary condition - Dirichlet, Neumann, and Robin - applied on boundary regions
. There are three possible types of boundary condition - Dirichlet, Neumann, and Robin - applied on boundary regions 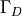 ,
, 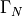 , and
, and 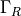 respectively.
respectively.
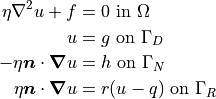
where 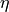 is a constant typically taken to be the diffusivity and
is a constant typically taken to be the diffusivity and 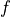 is some source function.
is some source function.
The different formulations of the Poisson equation finite element weak form are given below. Note that in all cases  is the trial function. In the case of the discontinuous Galerkin method,
is the trial function. In the case of the discontinuous Galerkin method, 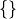 and
and ![[[]]](../_images/math/ef92a541da054ff2ee21f844d311b9b1f5a2b406.png) refer to the average and jump operators respectively and
refer to the average and jump operators respectively and 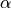 is the penalty coefficient. In the case of the diffuse interface method,
is the penalty coefficient. In the case of the diffuse interface method, 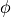 is the phase field,
is the phase field, 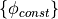 are masks for different boundary condition regions, and
are masks for different boundary condition regions, and 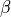 is the Nitsche method penalty parameter. Also note that for the diffuse interface method all integrals become volume integrals over the enclosing simple domain
is the Nitsche method penalty parameter. Also note that for the diffuse interface method all integrals become volume integrals over the enclosing simple domain  .
.
Standard Galerkin Finite Element Formulation
The standard Galerkin finite element method formulation is as follows:
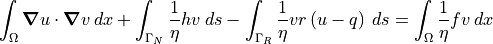
Dirichlet boundary conditions are imposed strongly by setting values at applicable boundary degrees of freedom.
Discontinuous Galerkin Formulation
The discontinuous Galerkin formulation is as follows:
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{\nabla} u \cdot \bm{\nabla} v \: dx \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \left( [[u\bm{n}]] \cdot \{ \bm{\nabla} v \} + [[v\bm{n}]] \cdot \{ \bm{\nabla} u \} - \alpha [[u]] [[v]] \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_D} \int_{\mathcal{F}} \left( \bm{n} \cdot \left( u - g \right) \bm{\nabla} v + \bm{n} \cdot v \bm{\nabla} u - \alpha \left( u - g \right) v \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_N} \int_{\mathcal{F}} \frac{1}{\eta} vh \: ds + \sum_{\mathcal{F} \in \mathcal{F}_R} \int_{\mathcal{F}} \frac{1}{\eta} vr\left( u - q \right) \: ds \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \frac{1}{\eta} fv \: dx](../_images/math/20d41f2e0e9c24402c42e0cd8417092ef3100ed5.png)
where volume integrals are over individual mesh elements 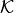 then summed over the entire triangulation
then summed over the entire triangulation 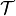 . Surface integrals are over mesh element facets
. Surface integrals are over mesh element facets 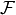 and summed over either interior facets
and summed over either interior facets 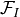 or boundary facets
or boundary facets 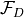 ,
, 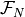 , and
, and 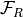 .
.
Diffuse Interface Formulation
The diffuse interface formulation is as follows for the standard Galerkin finite element method:
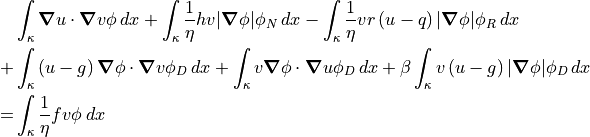
and for the discontinuous Galerkin method:
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{\nabla} u \cdot \bm{\nabla} v \phi \: dx \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \left( [[u\bm{n}]] \cdot \{ \bm{\nabla} v \} + [[v\bm{n}]] \cdot \{ \bm{\nabla} u \} - \alpha [[u]] [[v]] \right) \phi \: ds \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \left( u - g \right) \bm{\nabla} \phi \cdot \bm{\nabla} v + v \bm{\nabla} \phi \cdot \bm{\nabla} u + \beta \left( u - g \right) v \lvert \bm{\nabla} \phi \rvert \right) \phi_D \: dx \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \frac{1}{\eta} vh \lvert \bm{\nabla} \phi \rvert \phi_N \: dx + \sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \frac{1}{\eta} vr\left( u - q \right) \lvert \bm{\nabla} \phi \rvert \phi_R \: dx \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \frac{1}{\eta} fv \phi \: dx](../_images/math/bbeae358c711e15b2e3d9d069f6de920004fe92e.png)
Stokes Equations
The Stokes equations take the following form on a simulation domain 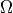 . There are two possible types of boundary condition - velocity Dirichlet and normal stress - applied on boundary regions
. There are two possible types of boundary condition - velocity Dirichlet and normal stress - applied on boundary regions 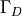 and
and 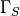 respectively.
respectively.
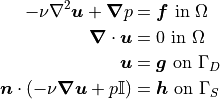
where 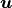 is the velocity and
is the velocity and 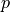 is the pressure. Furthermore,
is the pressure. Furthermore, 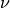 is the constant kinematic viscosity and
is the constant kinematic viscosity and 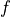 is some body force.
is some body force.
The different formulations of the Stokes equations finite element weak form are given below. Note that in all cases 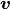 and
and 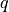 are the trial functions for velocity and pressure respectively. In the case of the discontinuous Galerkin method,
are the trial functions for velocity and pressure respectively. In the case of the discontinuous Galerkin method, 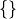 and
and ![[[]]](../_images/math/ef92a541da054ff2ee21f844d311b9b1f5a2b406.png) refer to the average and jump operators respectively and
refer to the average and jump operators respectively and 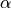 is the penalty coefficient. In the case of the diffuse interface method,
is the penalty coefficient. In the case of the diffuse interface method, 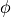 is the phase field,
is the phase field, 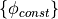 are masks for different boundary condition regions, and
are masks for different boundary condition regions, and 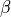 is the Nitsche method penalty parameter. Also note that for the diffuse interface method all integrals become volume integrals over the enclosing simple domain
is the Nitsche method penalty parameter. Also note that for the diffuse interface method all integrals become volume integrals over the enclosing simple domain  .
.
Standard Galerkin Finite Element Formulation
The standard Galerkin finite element method formulation is as follows:
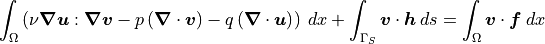
Dirichlet boundary conditions are imposed strongly by setting values at applicable boundary degrees of freedom.
Discontinuous Galerkin Formulation
The discontinuous Galerkin formulation is as follows:
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \: dx \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \nu \left( [[\bm{u}\bm{n}]] : \{ \bm{\nabla} \bm{v} \} + [[\bm{v}\bm{n}]] : \{ \bm{\nabla} \bm{u} \} - \alpha [[\bm{u} \bm{n}]] : [[\bm{v} \bm{n}]] \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_D} \int_{\mathcal{F}} \nu \left( \left( \bm{u} - \bm{g} \right) \bm{n} : \bm{\nabla} \bm{v} + \bm{v} \bm{n} : \bm{\nabla} \bm{u} - \alpha \left( \bm{u} - \bm{g} \right) \cdot \bm{v} \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_S} \int_{\mathcal{F}} \bm{v} \cdot \bm{h} \: ds \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \bm{f} \: dx](../_images/math/0052c0957ec534b25eaa78ecd47cfb584eddd339.png)
where volume integrals are over individual mesh elements 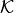 then summed over the entire triangulation
then summed over the entire triangulation 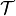 . Surface integrals are over mesh element facets
. Surface integrals are over mesh element facets 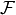 and summed over either interior facets
and summed over either interior facets 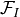 or boundary facets
or boundary facets 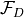 and
and 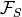 .
.
Diffuse Interface Formulation
The diffuse interface formulation is as follows for the standard Galerkin finite element method:
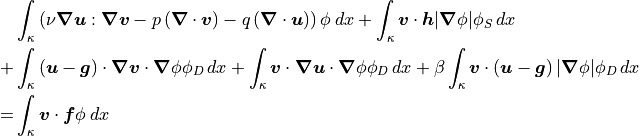
and for the discontinuous Galerkin method:
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \phi \: dx \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \nu \left( [[\bm{u}\bm{n}]] : \{ \bm{\nabla} \bm{v} \} + [[\bm{v}\bm{n}]] : \{ \bm{\nabla} \bm{u} \} - \alpha [[\bm{u} \bm{n}]] : [[\bm{v} \bm{n}]] \right) \phi \: ds \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \nu \left( \left( \bm{u} - \bm{g} \right) \bm{\nabla} \phi : \bm{\nabla} \bm{v} + \bm{v} \bm{\nabla} \phi : \bm{\nabla} \bm{u} - \beta \left( \bm{u} - \bm{g} \right) \cdot \bm{v} \lvert \bm{\nabla} \phi \rvert \right) \phi_D \: dx \\
- &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \bm{h} \lvert \bm{\nabla} \phi \rvert \phi_S \: dx \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \bm{f} \phi \: dx](../_images/math/a473c17d85a2f976f66710bfef5559021b462d1f.png)
Multi-Component Flow
Note
To be written once discontinuous Galerkin and diffuse interface formulations are available for the multi-component flow model.
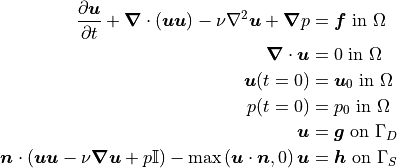
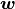 (usually the velocity from the previous time step).
(usually the velocity from the previous time step).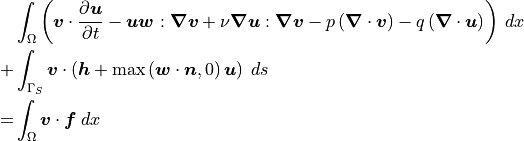
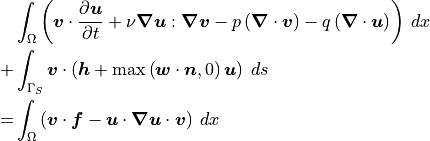
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \bm{v} \cdot \frac{\partial \bm{u}}{\partial t} - \bm{u} \bm{w} : \bm{\nabla} \bm{v} + \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \: dx \\
+ &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} [[\bm{v} \bm{n}]] : \left( \{ \bm{u} \} \left( \bm{w} \cdot \bm{n} \right) \bm{n} + \frac{1}{2} \left( \bm{u}^+ - \bm{u}^- \right) \lvert \bm{w} \cdot \bm{n} \rvert \bm{n} \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \nu \left( [[\bm{u}\bm{n}]] : \{ \bm{\nabla} \bm{v} \} + [[\bm{v}\bm{n}]] : \{ \bm{\nabla} \bm{u} \} - \alpha [[\bm{u} \bm{n}]] : [[\bm{v} \bm{n}]] \right) \: ds \\
+ &\sum_{\mathcal{F} \in \mathcal{F}_D} \int_{\mathcal{F}} \bm{v} \bm{n} : \left( \frac{1}{2} \left( \bm{u} + \bm{g} \right) \left( \bm{w} \cdot \bm{n} \right) \bm{n} + \frac{1}{2} \left( \bm{u} - \bm{g} \right) \lvert \bm{w} \cdot \bm{n} \rvert \bm{n} \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_D} \int_{\mathcal{F}} \nu \left( \left( \bm{u} - \bm{g} \right) \bm{n} : \bm{\nabla} \bm{v} + \bm{v} \bm{n} : \bm{\nabla} \bm{u} - \alpha \left( \bm{u} - \bm{g} \right) \cdot \bm{v} \right) \: ds \\
+ &\sum_{\mathcal{F} \in \mathcal{F}_S} \int_{\mathcal{F}} \bm{v} \cdot \left( \bm{h} + \max \left( \bm{w} \cdot \bm{n}, 0 \right) \bm{u} \right) \: ds \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \bm{f} \: dx](../_images/math/132e9c5888ca9c814681fac811126ee4c651c3a7.png)
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \bm{v} \cdot \frac{\partial \bm{u}}{\partial t} + \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \: dx \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \nu \left( [[\bm{u}\bm{n}]] : \{ \bm{\nabla} \bm{v} \} + [[\bm{v}\bm{n}]] : \{ \bm{\nabla} \bm{u} \} - \alpha [[\bm{u} \bm{n}]] : [[\bm{v} \bm{n}]] \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_D} \int_{\mathcal{F}} \nu \left( \left( \bm{u} - \bm{g} \right) \bm{n} : \bm{\nabla} \bm{v} + \bm{v} \bm{n} : \bm{\nabla} \bm{u} - \alpha \left( \bm{u} - \bm{g} \right) \cdot \bm{v} \right) \: ds \\
+ &\sum_{\mathcal{F} \in \mathcal{F}_S} \int_{\mathcal{F}} \bm{v} \cdot \left( \bm{h} + \max \left( \bm{w} \cdot \bm{n}, 0 \right) \bm{u} \right) \: ds \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \bm{v} \cdot \bm{f} - \bm{u} \cdot \bm{\nabla} \bm{u} \cdot \bm{v} \right) \: dx](../_images/math/fbd009710b1cfebd08a346097d3b74fda9bf0faf.png)
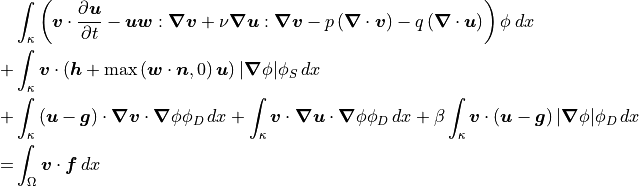
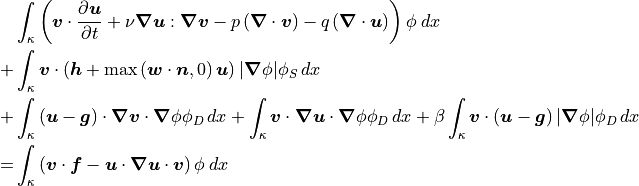
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \bm{v} \cdot \frac{\partial \bm{u}}{\partial t} - \bm{u} \bm{w} : \bm{\nabla} \bm{v} + \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \phi \: dx \\
+ &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} [[\bm{v} \bm{n}]] : \left( \{ \bm{u} \} \left( \bm{w} \cdot \bm{n} \right) \bm{n} + \frac{1}{2} \left( \bm{u}^+ - \bm{u}^- \right) \lvert \bm{w} \cdot \bm{n} \rvert \bm{n} \right) \: ds \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \nu \left( [[\bm{u}\bm{n}]] : \{ \bm{\nabla} \bm{v} \} + [[\bm{v}\bm{n}]] : \{ \bm{\nabla} \bm{u} \} - \alpha [[\bm{u} \bm{n}]] : [[\bm{v} \bm{n}]] \right) \: ds \\
- &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \left( \frac{1}{2} \left( \bm{u} + \bm{g} \right) \left( \bm{w} \cdot \bm{\nabla} \phi \right) + \frac{1}{2} \left( \bm{u} - \bm{g} \right) \lvert \bm{w} \cdot \bm{\nabla} \phi \rvert \right) \phi_D \: dx \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \nu \left( \left( \bm{u} - \bm{g} \right) \bm{\nabla} \phi : \bm{\nabla} \bm{v} + \bm{v} \bm{\nabla} \phi : \bm{\nabla} \bm{u} - \alpha \left( \bm{u} - \bm{g} \right) \cdot \bm{v} \lvert \bm{\nabla} \phi \rvert \right) \phi_D \: dx \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \left( \bm{h} + \max \left( \bm{w} \cdot \bm{n}, 0 \right) \bm{u} \right) \lvert \bm{\nabla} \phi \rvert \phi_D \: dx \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \bm{f} \phi \: dx](../_images/math/0e7bcde6ddc4912c801e3b7a65bb232cc3920213.png)
![&\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \bm{v} \cdot \frac{\partial \bm{u}}{\partial t} + \nu \bm{\nabla} \bm{u} : \bm{\nabla} \bm{v} - p \left( \bm{\nabla} \cdot \bm{v} \right) - q \left( \bm{\nabla} \cdot \bm{u} \right) \right) \phi \: dx \\
- &\sum_{\mathcal{F} \in \mathcal{F}_I} \int_{\mathcal{F}} \nu \left( [[\bm{u}\bm{n}]] : \{ \bm{\nabla} \bm{v} \} + [[\bm{v}\bm{n}]] : \{ \bm{\nabla} \bm{u} \} - \alpha [[\bm{u} \bm{n}]] : [[\bm{v} \bm{n}]] \right) \phi \: ds \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \nu \left( \left( \bm{u} - \bm{g} \right) \bm{\nabla} \phi : \bm{\nabla} \bm{v} + \bm{v} \bm{\nabla} \phi : \bm{\nabla} \bm{u} - \alpha \left( \bm{u} - \bm{g} \right) \cdot \bm{v} \lvert \bm{\nabla} \phi \rvert \right) \phi_D \: dx \\
+ &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \bm{v} \cdot \left( \bm{h} + \max \left( \bm{w} \cdot \bm{n}, 0 \right) \bm{u} \right) \lvert \bm{\nabla} \phi \rvert \phi_S \: dx \\
= &\sum_{\mathcal{K} \in \mathcal{T}} \int_{\mathcal{K}} \left( \bm{v} \cdot \bm{f} - \bm{u} \cdot \bm{\nabla} \bm{u} \cdot \bm{v} \right) \phi \: dx](../_images/math/09b44805661887868187b9b7f5620a1cef93d266.png)